コンデンサ
- C:静電容量/電気容量/キャパシタンス[F][C/V]・・・
- コンデンサにおいて、1Vの電圧を与えて1Cの電荷を蓄えた時の静電容量が1F。
- 10-12がpF(ピコファラド)。
- C = ε\(\large{\frac{S}{d}}\)(Sは平行板面積、dは距離)
- コンデンサ内は一様な電場なので、V=Ed(Vは電圧、Eは電場、dは極板間の距離)
- コンデンサ内の電荷総量をQ[C]とすると、コンデンサから出る電気力線の数(E*S)は、ガウスの法則より、
\(\large{\frac{Q}{ε}}\)=4πkQ[本](電荷Qが決まれば自動的に本数は決まる)
ES=4πkQ=V\(\large{\frac{S}{d}}\)[本]
Q=V\(\large{\frac{S}{4πkd}}\)=Vε\(\large{\frac{S}{d}}\)
となり、ε\(\large{\frac{S}{d}}\)を静電容量Cとすると、おなじみのコンデンサに蓄えられる電荷の式
Q=CV
が出来上がる。 - コンデンサの役割は、直流を遮断し交流を通す(ノイズ除去等)作用、平滑作用(交流で整流した脈流を蓄えた電流を流して平滑する)、力率改善作用(コイルの位相を揃える)等がある。
- 直流ではもちろん電流は流さないが、交流では蓄えた電荷を流すので電流が流れると表現される
- コンデンサの静電容量が小さいと交流の電圧が最大値になる前に充電が完了してしまい、その時点で電流が止まる。
- 同じ静電容量のコンデンサなら、交流の周波数が高いほうが電流が流れやすい。
- コンデンサは交流の電流を制限するため、抵抗と同じように作用する。
- コンデンサの疑似抵抗(容量リアクタンスXCは、交流の周波数に反比例する。リアクタンスは交流周波数が増えれば低くなるので電流が流れやすくなる。
- XC:容量性リアクタンス・・・XC=\(\large{\frac{1}{jωC}}\)(jは虚数単位=2乗すると-1になる数)
直流の場合、コンデンサに流れ込む電流(電荷)は最初が一番高く、電荷が溜まりコンデンサの逆向きの電圧が高くなってくると、電流は弱まっていき、電荷が溜まりきるとコンデンサの電圧が電源電圧に等しくなり、電流は0になる。
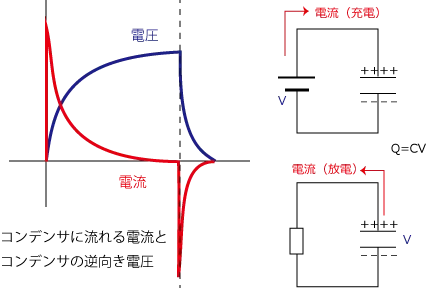
コンデンサの定格電圧よりも電源の電圧が低いときは、コンデンサが満タンにならずに放電されるが、定格電圧を電源の電圧が超える場合は、蓄えられる電圧をオーバーするので壊れる恐れがある(一般的には定格の2.5倍程度までは耐えられるらしい)。
交流の場合、交流のインピーダンスのページでの説明にあるように、電圧に対して電流の位相が90°進む。
また、コンデンサに流れる電流I=C\(\large{\frac{dV}{dt}}\)より、コイルと少し考え方が違って、電圧の時間変化が電流の増加を引き起こすため、電圧の変化が最大の時、電流が最大or最小となり、電圧の変化が0の時、電流が0となる。
周波数が高い電流はコイルを通しにくいが、コンデンサは通しやすい。
コンデンサに電流が流れているように見えるのは、コンデンサが充電と放電を繰り返す場合、つまり交流に限る。そのため、コンデンサは交流は通し、直流は通さないという表現をされる。
この特徴を生かして、直流成分によるノイズの除去や、ダイオードとコイル、コンデンサを使った平滑回路等に利用されている。
コンデンサの等価回路
コンデンサは容量性リアクタンスとしての抵抗成分とは他に、導線の抵抗R、コイルじゃないのにインダクタンスLを持っている。
コイルに限らず、コンデンサも等価回路を持つため、周波数を上げていき、自己共振周波数=f=\(\large{\frac{1}{2π\sqrt{LC}}}\)[Hz]でインピーダンスは抵抗Rのみとなり、それを超えると、コンデンサとしての機能が失われ(容量性リアクタンスはなくなり)、誘導性リアクタンスが周波数の上昇とともに増加していく。
つまり、コンデンサなのにインピーダンスが上昇していき、電流が低下する。
(詳しくはパナソニックのページ参照。かなりよくまとまってる。)

