マクスウェル方程式
マクスウェルの4つの方程式は、電磁気学の電場と磁場の関係式をまとめたもの。積分形は難しいので微分形のみ。
| 電場E or 電束密度D | 磁場H or 磁束密度B | |
|---|---|---|
| divergence (湧き出し) |
divD=ρ or divE=\(\large{\frac{ρ}{ε_0}}\) |
divB=0 |
| rotation (回転) |
rotE=-\(\large{\frac{dB}{dt}}\) | rotH=\(\large{\frac{dD}{dt}}\)+j or rotB=μ0(ε0\(\large{\frac{dB}{dt}}\)+j) |
divD=ρ
電場に関するガウスの法則。
【電束密度Dの湧き出しは、電荷密度ρ(単位体積当たりの電荷量=C/m3)と等しい】の意味。
電束密度Dは電場Eに誘電率εをかけることで変換できるので、divD=ρは、divE=\(\large{\frac{ρ}{ε_0}}\)に変換できる。
divDは、電束密度の湧き出し=∇(ナブラ)Dのことで、つまり、各方向(x,y,z)の微小体積から出ていく電束線を合計したもの(\(\large{\frac{dD}{dx}}\)+\(\large{\frac{dD}{dy}}\)+\(\large{\frac{dD}{dz}}\))を略した形。
ガウスの法則とは?
【誘電率εの媒質中で、ある閉曲面を垂直に貫く電気力線の本数は閉曲線内部に存在する電荷だけ(閉曲面外部の電荷は閉局面を入って出るで±0として無視できる)の総量Qに比例し、\(\large{\frac{Q}{ε}}\)(=4πkQ)[本]に等しい。】ということ。
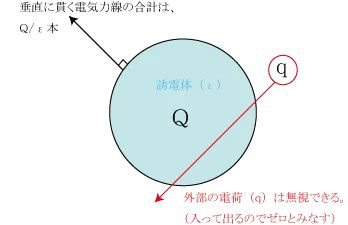
Q[C]の電荷、1㎡あたりE本の電気力線が出ているとすると、総電気力線数N[本]は、N=E*S(Eは電場、Sは表面積)。
ガウスの法則より、ES=\(\large{\frac{Q}{ε}}\)となる。
点電荷では電荷を球体として考えるので、表面積は4πr2、εは\(\large{\frac{1}{4πk}}\)なので、
E*4πr2=\(\large{\frac{Q}{ε}}\)=4πkQ[本]
E=k\(\large{\frac{Q}{r^2}}\)[N/C]or[V/m]
となり、点電荷のクーロンの法則を導くことができる。
また、電場の中で電荷が受ける力は、F=qEで示せるので、電荷qが電荷Qが作る電場から受けるクーロン力は、qをかけて
F=k\(\large{\frac{qQ}{r^2}}\)[N]となる。
また、1[C]の電荷を電荷Qからr[m]だけ離れたところに置いた時の電位Vは、1[C]とrをかけて
V=k\(\large{\frac{Q}{r}}\)[J/C]となる。
さらに、q[C]の電荷をの電荷をQからr[m]だけ離れたところに置いた時の位置エネルギーUは、U=qVより
U=k\(\large{\frac{qQ}{r}}\)[J]となる。
divB=0
磁場に関するガウスの法則。
【点電荷に対応する単磁荷(モノポール)は存在しない】の意味。
磁石のNとSは単独で切り離せず、N極の磁束線は点電荷のように無限遠には広がらず、必ずS極へ向かい、磁束はループしているという事。
divBは∇Bであり、各方向の磁束密度の湧き出しはループしてしまうので結果0となる。
rotE=-\(\large{\frac{dB}{dt}}\)
ファラデーの電磁誘導の法則を任意の閉曲面に対して適用できるようにしたのがマクスウェルの式。"向き"については、レンツの法則とフレミングの右手の法則が該当する。
レンツの法則は、【何かが原因(磁束密度の変化等)で(コイル等に)誘導電流が発生する場合、発生した誘導電流の向きは、原因を妨げる方向】という法則
【磁束密度の時間変化は渦電流を発生させる】の意味。
コイルに磁石を近づけていく(or磁場の中でコイルを貫く磁束密度が変化する方向にコイル等の導体を動かす)と、レンツの法則により、磁石を遠ざける方向(マイナス)に磁場が発生し、誘導起電力が発生し、電流が流れる。
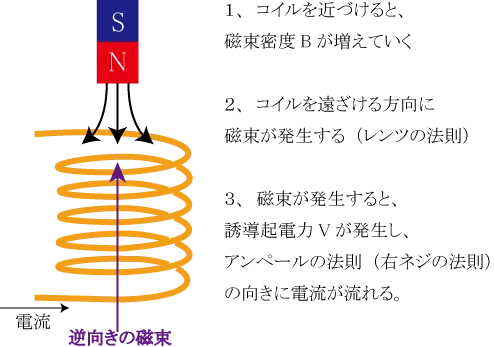
重要なのは、電流が流れていない状態→電流を流す(起電力を発生させる)状態にするケースを言っているということ。
なので、フレミングで言えば、"電磁力"の磁場と力が分かっていて、電流が分からない状態を指す。
rotEは∇Eであり、回転方向のベクトルの合計で、元は行列である。
なお、この時に生じる誘導起電力は、コイルの巻き数をNとすると、
V=-N\(\large{\frac{dφ}{dt}}\)[V]
と表すことができる。この式が電磁誘導の基本の式となる。
これを一様な磁場の中でコイルを貫く磁束密度を変化させる以下のケースで考えると、(同じことなのに見方が違うだけで同じに見えないのが難しいところ)
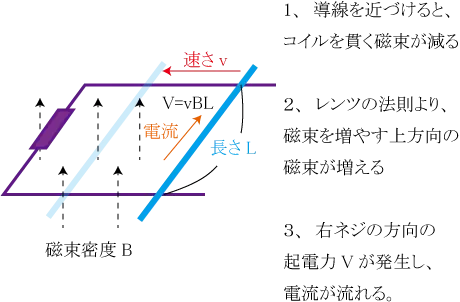
動く導体棒に生じる起電力Vは、導体棒を動かす速度をv、磁束密度をB、導体棒のコイルを構築する部分の長さをLとすると、
V=vBL[V]
と表せる。
コイルの巻き数は1なので、V=-\(\large{\frac{dφ}{dt}}\)[V]とした後、φ=BS(Bは磁束密度、Sは面積)=vBLΔtを代入して導く。
また、誘導起電力Vはコイルの自己インダクタンスをL[H]とすると、
V=-L\(\large{\frac{dI}{dt}}\)[V]・・・自己インダクタンスLに電流Iの時間変化をかけたもの。
とも表すことができる。
ローレンツ力とフレミングの左手の法則
この二つは、先と違って、電流と磁場があるときに導体が受ける力の向き(フレミング)と大きさ(ローレンツ)について表すもの。
つまり、フレミングで言うと、電磁力の電流と磁場が分かっていて、力がわからない状態が該当する。そして、この時にフレミングは右手ではなく左手を使う。
という感じで、電流と磁場があると力(ローレンツ力)を受けるわけで、磁場の中で動いている電荷に生じるこの力を求める式が、
F=qvB・・・q[C]の電荷を磁束密度Bの中を速度vで動かすときに受ける力の大きさ
と、
F=IBL・・・コイルを貫く磁束密度がB[T]の時に、長さL[m]の導線に、電流I[A]を流した時に、導線が受ける力の大きさ
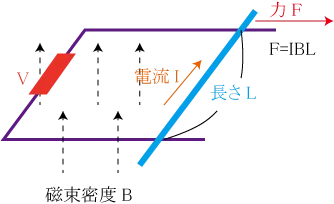
である。
速度vで動かせば、磁束密度が変化するので、電場が生じて電流が流れる。F=IBLはF=qvBを変形した式。
力Fの向きは、フレミングの左手の法則で求めてもいいし、右ネジの法則(電流の向きを磁場の向きの方向に折りたたんだ時の親指の向きが力の向き)を使ってもいい。
qが-の電荷の時は、速度vは電子の向きとなり、電流の向きは逆向きであることに注意する。
rotH=\(\large{\frac{dD}{dt}}\)+j
マクスウェル-アンペールの法則。
rotH=j の部分がアンペールの法則(電流が流れると渦状の磁場が発生するという右ネジの法則の正式名称)。
右ネジの法則では、流す電流が直線状か、渦(ソレノイド=コイル内等)状かで、親指の向きは変わる。電流が直線状なら親指が電流だし、電流がソレノイド内なら親指が磁場の向きとなる。
jは電流密度[A/㎡]で単位面積に垂直方向、単位時間に流れる電流。j=σE(σ:導電率)
コイルに鉄心を入れた状態で電流を流すと、鉄心中の電子の自転の向きが揃うので、磁場(厳密には磁束密度かな)は入れないときに比べてかなり増強される。(透磁率μの高い強磁性体の金属は鉄、コバルト、ニッケルだけ)
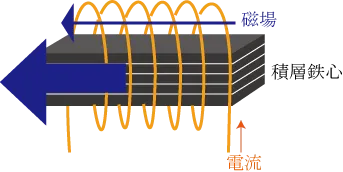
入れる鉄心は、交流のように電流が変化するモータ等においては特に、ヒステリシス損失と呼ばれる熱エネルギー損失が少ない鉄にケイ素を混合した電磁鋼のような軟磁性体を用い、合わせて渦電流損失を抑えるために、渦電流が流れる経路を小さくするために積層構造にすることが望ましい。
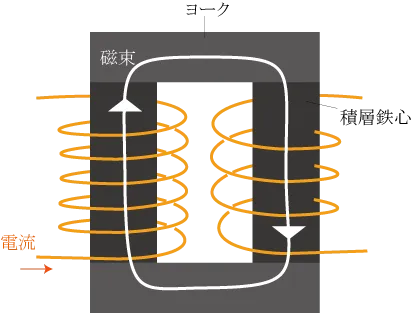
また変圧器では電磁誘導によって生じた磁束が空気中に逃げないように、鉄心同士を強磁性体(ヨークと呼ばれる)でつなげた構造となっている。
わき道にそれたが話を戻して、今度はマクスウェルが追加した、\(\large{\frac{dD}{dt}}\)の部分について。
【電束密度の時間変化も、アンペールの法則と同じように渦状の磁場を発生させる】というもの
この場合はレンツの法則のような逆向きの磁場を考えるわけではないので、-(マイナス)はつかない。
そして、先のアンペールの法則と合わせて、マクスウェル-アンペールの式として整理されている。

