微分と積分
微分と積分がたまに出てくると忘れてることが多いのでメモ。
微分とは
微分とは、ある関数\(f(x)\)の、ある時点での変化の割合や傾きを表すものであり、導関数\(f'(x)\)を求めることである。
ここでfはfuncitonの意味で関数を表し、f(x)は、xを入力として与えた時の出力を表す。この出力はyとも表せるが、yで表すよりもf(x)という任意のxに対する返り値の形で表した方が実用的である。
導関数\(f'(x)\)は以下のようにして求められる。
\(\begin{eqnarray} f'(x) = \frac{ dy }{ dx } = \lim_{ \Delta x \to 0 } \frac{ f(x + \Delta x) - f(x) }{ \Delta x } \end{eqnarray}\)
この関数の意味は、\(y=f(x)\)という関数のxを微小に変化(dxだけ変化)させた時のyの変化のことで、\(\frac{ dy }{ dx }\)とも表せる。
ここで、関数\(f(x)=2x\)という一次関数を例にすると、xの変化量をΔxとすれば、yの微小変化量はf(x+Δx)-f(x)となり、Δxを限りなく0に近づけた時のyの値は、 \(\large{\frac{ 2(x+Δx)-2x }{ Δx }}\)となり、Δxは約分されて答えは2となる。
これはΔxがどんな値で、どこからどこまでの範囲をとってもxの変化量に対するyの変化量は常に2倍であることを示している。言い換えれば、ここで言う2という値は増加の割合や増加の速さとも言える。
とはいえ、自転車のスピードメーターが、走行速度を知りたいときに、車輪が1周回るのに何秒かかるかを計測して、速度を求めるときには、ある一定の時間(車輪が1周回るのに要する時間)は等速直線運動しているという仮定の下に計算するので、「はじき」を使って一定時間の傾き求めれば事足りる。
電圧=電流×抵抗やPv=nRTについても同様だが、完全に比例関係になっているような場合は、微分という概念を考えない方がすっきりと理解できる。
円の面積πr2をrについて微分する(\(\large{\frac{ d }{ dr }}πr^2\))と円周の長さ2πrが導き出せるが、これは半径rが微小だけ増加した時の面積の増加量の割合を示しているに過ぎないため、円周を求めるのに円の面積を微分しようとはあまり思わない。円柱の体積を微分すると側面積になることも同様。
ならば微分をすることの意味は?
意味を理解するには、傾きが時間とともに変化するような挙動をする状態を考えといい。このようなケースでは傾きが0になる場所(変曲点)が最大値や最小値になることが多く、それらを求めることがその関数が示す事象の最大効率や最も効率の悪くなる点を知ることにつながる。これが微分の本来の目的である。
速さが常に一定の場合は傾きが0になることがないので、微分のメリットはあまり感じられない。
例1 四角形の最大の面積
例として、
長さ10mのロープで四角形を作る場合、最大の面積になるのは縦横が何mの時か?を考えた時、面積をf(x)、横の長さをxとすると、関数f(x)は、\(f(x)=(10-x)*x=10x-x^2\)となる。
二次関数のグラフなので、この関数の傾きは常に一定ではないことがわかる。
そこで、この関数をxについて微分すると、\(f'(x)=-2x+10\)となり、傾きが0、つまり\(f'(x)=0\)となるxは5であることがわかる。
よって、縦5m、横5mの時に最大の面積25㎡となることがわかる。
例2 車の燃費がもっともよい速度
もう一つ、車の燃費が最もよい走行速度を算出する例を考える。
これを求めるためには、燃費と速度の関数を作成しなければならず、作成するためには以下の手順を考慮することができる。
- データ収集・・・実際の車両やテストベッドを使用して、異なる速度での燃費。このデータ収集は、一定の条件下(例:平坦な道路、一定の気温、エンジンの状態など)で行われることが多い。
- データのプロット・・・収集したデータを速度と燃費のグラフにプロット。
- 関数の選択・・・データの傾向に基づいて、最も適切な関数形を選択する。例えば、2次関数、3次関数、対数関数など。一般的には、低速から中速までの範囲で燃費が向上し、ある速度を超えると燃費が悪化するという特性が考えられるため、2次関数や3次関数が適用されることが多い
- 関数のフィッティング・・・収集したデータに基づいて、選択した関数をフィッティング。フィッティングは、最小二乗法などの手法を使用して行われることが多い。最小二乗法は、統計学や数学において、データへのモデルの適合度を最適化するための一般的な手法であり、観測データとモデルの予測との間の差(残差)の二乗和を最小にするパラメータを求める
- 関数の検証・・・実際の燃費データとフィッティングした関数との間の誤差を評価する。
- 関数の使用・・・フィッティングした関数を使用して、任意の速度での燃費を予測するが、実際の運転状況や外部環境によって燃費は大きく変動するため、作成した関数はあくまで参考の一つとして使用する
燃費の関数ができたら、それを速度で微分すれば、速度の変化が0になる場所が燃費が最も悪いかよいかの速度であることがわかります。
一つ一つ点を打ってつなげてグラフにしてしまえば目視だけで最高効率になる点がわかりそうですが、、、。
積分とは
積分とは、ある関数で囲まれた面積を求めることで、原始関数(微分すると元の関数になる関数)を求めることである。
積分には、以下の二つのタイプがある。
- 定積分・・・関数のグラフとx軸、および2つの垂直線で囲まれた領域の面積を求めるもの。\(\int_a^b f(x) dx\)は関数f(x)の区間a,bにおける面積を示している。
- 不定積分・・・関数の原始関数を求めるもの。例として、\(f(x)=x^2\)の原始関数を考えると、\(\large{F(x)=\frac{1}{3}x^3+C}\)となる。Cは積分定数と呼ばれ、任意の定数をとることができるが、定積分では打ち消されて0になるので考えない。 ある関数の原始関数を求めることが積分の最初のステップであり、原始関数を求めることができなければ積分は解けない。原始関数を求めることのできる形にもっていくために、部分積分や置換積分を用いる。
例として、\(\int_a^b f(x) dx\)というf(x)の区間a,bにおける面積\(f'(x)\)を求める方法について説明すると、
囲まれた面積を微小な幅(dx)の四角形の集まりであると考えて、それらを足し合わせて面積を求める。四角の集まりだと曲線をはみ出る部分が誤差になってしまうが、dxを限りなく0に近づければ線となり、四角形ではなく線の集まりであれば面積と同じと考えることに抵抗はなくなる。
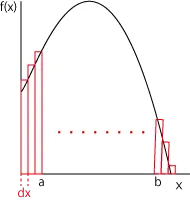
この幅dxで高さがf(x)の面積は縦×横でf(x)×dxとなり、これをaからbまで足し合わせたものを表すのが、\(\int_a^b f(x) dx\)である。
理由はさておき、微分するとこの式になる関数=原始関数\(F(x)\)を求めて、その原始関数にbを代入して得られた数から、aを代入して得られた数を引くと、この定積分の答え、すなわち面積を導き出すことができます。
\(\int_a^b f(x) dx=F(b)-F(a)\)
f(x)×0.000.....1+f(x)×0.000.....1+......みたいな感じで区間a,b全体で足し合わせたものは、微分するとこの関数になる関数(原始関数)を求めてその差\(F(b)-F(a)\)を計算すると導き出せるというわけです。この関係は、微分と積分が逆の操作であるという基本的な熱力学の原理に基づいている。
値を代入して引き算することはさほど難しいことではないので、積分で重要なのはこの原始関数をいかにして求めるか、つまり定積分ではなく不定積分)であるため、大学入試では不定積分をどのようにして解くかが問題となっている。
普段簡単な図形の面積を求めているときに積分を解いていると認識することは少ないと思うが、四角形や三角形の面積も積分で求めることが出来る。
例1 四角形の面積
1片が10㎝の四角形は、f(x)=10という関数で示すことが出来て、例えば1と5に囲まれた面積を求めたいなら、\(\int_1^5 10dx\)を求めればよく、\(10x+C\)という原始関数に数値を代入すると、\(10*5+C-10*1+C=40\)という感じで答えを導き出せる。
例2 三角形の面積
傾きが2の直線は、\(f(x)=2x\)という一次関数で表せる。例えばxが0から10までの面積を積分で求めようとすると、\(\int_{0}^{10} 2xdx\)と表すことができる。原始関数は\(x^2\)なので、\(10^2-0^2\)となって、1辺が10で傾きが2、面積が100の三角形が求められる。三角形の公式で導き出せる答えと同じである。
例3 円の面積
円の面積は、円の方程式が\(x^2+y^2=r^2\)であることを利用して、これをyについて解くと、\(y=\sqrt{r^2-x^2}\)。これは原点を中心とした半径rの円の上半分を表す。この関数を区間[-r,r]で積分することで、円の上半分の面積を求めることができ、2倍すると円全体の面積を求めることができる。\(\int_{-r}^{r} \sqrt{r^2-x^2}dr\)
これを積分すると、円の面積は、\(2×\left[ \frac{x}{2}\sqrt{r^2-x^2}+\frac{r^2}{2}arcsin(\frac{x}{r}) \right]_{-r}^{r}\)=\(πr^2\)となり、円の面積の公式と一致する。
このようにして、公式が存在してるものの面積はもちろんのこと、公式が存在しない曲線で囲まれた面積でも、原始関数を積分により導き出すことができれば、求めることが可能となる。
実生活では、以下のような場面で役立っている。
- 電力の使用量:家庭の電力メーターは、電流(または電力)を時間に対して積分することで、消費された総電力量(kWh)を計算しています。
- 流量計:水道のメーターやガスのメーターは、流れる流体の流速を積分して、総流量を計算しています。
- 経済学における消費者余剰と生産者余剰:需要曲線や供給曲線の下の面積を積分することで、消費者余剰や生産者余剰を計算することができます。
- 医療分野の放射線治療:放射線の線量分布を積分することで、特定の領域にどれだけのエネルギーが供給されたかを計算することができます。

